Eine Erklärung zum Maßstab und wie human being diesen umrechnet, lernt ihr hier. Dies sehen wir uns an:

  • Eine Erklärung, wofür man einen Maßstab braucht.
  • Beispiele zum Umrechnen von Maßstäben (auch Textaufgaben).
  • Aufgaben / Übungen damit ihr dies selbst üben könnt.
  • Ein Video zu Maßeinheiten als Grundlage.
  • Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Ihr solltet wissen, was Zentimeter, Meter und Kilometer sind. Wer davon keine Ahnung hat, sieht bitte in Längeneinheiten umrechnen rein.

Erklärung Maßstab

Zeichnet ein Architekt ein Haus auf dem Papier oder elektronisch, dann ist die Zeichnung deutlich kleiner als in der Realität. Dies gilded auch für Landkarten: Hier wird die Realität deutlich kleiner dargestellt. Nur wie viel kleiner wird etwas dargestellt? Dies gibt man mit dem Maßstab an.

In manchen Fällen wird etwas auch vergrößert. Sieht man sich ganz kleine Objekte - zum Beispiel unter dem Mikroskop an, dann ist es möglich, diese deutlich größer auf Papier oder einem Bildschirm darzustellen. Wie viel größer etwas dargestellt wird, gibt man ebenfalls mit einem Maßstab an.

Definition Maßstab:

Hinweis:

Der Maßstab gibt an, wie stark etwas vergrößert oder verkleinert wird. Es handelt sich dabei um zwei Zahlen, zwischen denen ein Doppelpunkt steht.

Beispiel Maßstab Verkleinerung:

Auf einer Landkarte steht als Maßstab 1 : 50000. Wie viel sind 2 Zentimeter auf der Landkarte in der Realität?

Lösung:

Der Maßstab 1 : 50000 bedeutet, dass 1 cm auf der Landkarte in der Realität 50000 Zentimeter sind. Um von i cm auf two cm, müssen wir mit ii multiplizieren.

Maßstab Beispiel Verkleinerung

Damit entsprechen 2 Zentimeter auf der Landkarte in Realität 100.000 cm (umgerechnet one.000 Meter oder 1 Kilometer).

Beispiel Maßstab Vergrößerung:

Auf einem Plan ist ein Computerchip xviii Zentimeter breit. Der Plan ist im Maßstab 40 : 2. Wie breit ist der Chip?

Lösung:

Der Maßstab 40 : ii bedeutet, dass 40 cm auf dem Programme in der Realität 2 cm sind. Wir möchten jedoch nicht wissen, wie viel twoscore cm auf dem Plan sind, sondern wie viel nur 18 cm sind. Und was genau dies in der Realität ist. Daher schreiben wir uns zunächst dies auf:

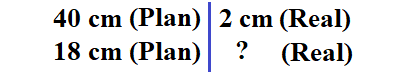
Maßstab Vergrößerung Beispiel

Um von xl cm auf 18 cm zu kommen, müssen wir mit 18:xl multiplizieren. Dies tun wir auf beiden Seiten.

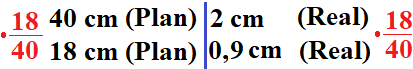
Maßstab Beispiel Vergrößerung B

Der Chip ist in der Realität 0,9 cm breit.

Anzeige:

Beispiele Maßstab

In diesem Abschnitt sehen wir uns noch Textaufgaben (Sachaufgaben) zum Maßstab an.

Beispiel 1:

Auf einer Karte für Flugzeuge gilt ein Maßstab von ane : 500.000. Zwischen zwei Flugplätzen ist ein Abstand von 5 cm zu messen. Wie groß ist dice Entfernung in Kilometer in Wirklichkeit?

Lösung:

1 cm auf dem Plan sind 500.000 cm in der Realität. Von ane cm auf 5 cm kommt human mit der Multiplikation mit five.

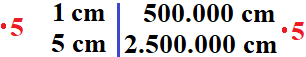
Maßstab Beispiel 1

Damit kommen wir auf 2.500.000 cm. Dies sind 25.000 m oder auch 25 km.

Beispiel 2:

Zwei Bahnhöfe sind in der Realität x Kilometer von einander entfernt. Diese Entfernung soll auf einer Karte im Maßstab 1:25.000 eingetragen werden. Wie viel Zentimeter ist der Abstand der Bahnhöfe auf der Karte?

Lösung:

1 Zentimeter auf der Karte sind 25.000 Zentimeter in existent. Dice 25.000 Zentimeter rechnen wir zunächst um in 250 Meter bzw. 0,25 Kilometer. Wir wissen damit, dass 1 cm auf dem Programme in der Realität 0,25 km sind. Um die Länge auf der Karte zu berechnen, müssen wir daher mit ten : 0,25 multiplizieren.

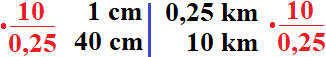
Maßstab Beispiel 2

Auf der Karte sind die beiden Bahnhöfe 40 cm entfernt voneinander.

Beispiel iii:

Eine Wohnung wurde im Maßstab i : 100 gezeichnet. Was ist in der Wirklichkeit 100 mal and then groß? Die Längen oder dice Flächen?

Lösung:

  • Der Maßstab bezieht sich auf die Längen bei einem Programme. 1 cm auf dem Plan sind 100 cm in der Realität.
  • Eine Fläche erhält man, indem man Länge mit Breite multipliziert.
  • Ein Quadrat auf dem Plan wäre zum Beispiel 1 cm · 1 cm = 1 cmii groß
  • In der Realität sind dies 100 cm · 100 cm = x.000 cmii.

Von one cm2 auf x.000 cm2 ist ein Faktor 10.000 oder auch 1:10.000. Wer es nicht glaubt, nimmt ein Quadrat mit 10 cm · 10 cm = 100 cm2 oder im Vergleich dazu in Realität thousand cm · 1000 cm = ane.000.000 cm2.

Übungen / Aufgaben Maßstab

Anzeigen:

Video Längeneinheiten

Grundlagen Maßeinheiten

Um Maßstäbe umrechnen zu können, ist es sehr hilfreich, wenn man verschiedene Längeneinheiten kennt. Zu den Längeneinheiten gehören zum Beispiel Zentimeter, Meter, Kilometer und einige andere. Wie dies funktioniert lernt ihr im nächsten Video:

Nächstes Video »

Fragen mit Antworten zum Maßstab

In diesem Abschnitt geht es um typische Fragen mit Antworten zum Maßstab.

F: Welche Maßstäbe sind typisch?

A: Eine kleine Übersicht ganz kleiner Maßstäbe (als Ersatz zu einer Tabelle):

  • 1 : 5
  • one : 100
  • 1 : xx
  • i : thou
  • 1 : 1
  • ane : 50

F: Gibt es eine einfache Formel für Maßstäbe?

A: In vielen Büchern wird einfach mit einer Zahl multipliziert oder dividiert, um mit dem Maßstab zu rechnen. Daraus könnte homo eine Formel machen. Jedoch hilft dies wenig, wenn man anspruchsvolle Textaufgaben lösen muss. Denn genau hier ist Verständnis für ein Thema nötig und nicht einfach ein Einsetzen in eine Formel.

F: Wann wird dieses Thema in der Schule behandelt?

A: Manchmal wird dieses Thema schon ein bisschen in der Grundschule behandelt. Then richtig kommt dieses Thema jedoch erst in der 5. Klasse oder half dozen. Klasse.